Abstract
This article examines the discovery of non-Euclidean and higher-dimensional geometries in the latter part of the nineteenth century.
In 1884, a modest theologian-cum-schoolteacher, Edwin A. Abbott, anonymously published Flatland, an odd little parable treating an imaginary world of two dimensions and the flat geometrical shapes who live there. The narrator of the tale, whose name is simply A Square, relates how he is visited by an emissary from the world of three dimensions, a Sphere, and gradually comes to understand the limitations of his own perceptions. After attempting unsuccessfully to enlighten his fellow Flatlanders regarding the existence of higher dimensions, he is imprisoned for sedition for the rest of his life. The story ends with him admitting that he is gradually beginning to lose his ability to hold onto faith in the third dimension.
The ostensible subject of Abbott’s novel is the discovery of non-Euclidean and higher-dimensional geometries in the latter part of the nineteenth century: geometries that either posit the existence of more than three spatial dimensions or deny the parallel postulate. The two new “schools” of geometry are often confused, but the two challenges to traditional mathematics have different philosophical implications, so they will be discussed here separately.
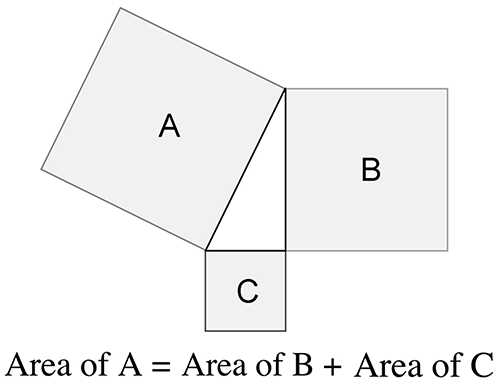
n-Dimensional Geomety: Throughout the early decades of the nineteenth century, reformers of the ![]() Cambridge Tripos examination in Mathematics[1] debated the extent to which analytic algebra should be included in the exam alongside Euclidean geometry and applied mathematics. Euclidean geometry treats the properties of shapes as they (arguably) exist in the real world. Analytic algebra, invented by Descartes in the 17th century, expresses (arguably) these same truths in mathematical form; that is, the formulas of Cartesian algebra were conceived by most Victorians merely as a translation, or symbolic representation, of the truths already expressed in different form by Euclid. For example, one could express the Pythagorean Theorem as shapes subject to a “proof by rearrangement”; that is, one could measure the physical area of the relevant squares to show that, in fact, the area of square a is equal to that of squares b plus c (Fig. 1).
Cambridge Tripos examination in Mathematics[1] debated the extent to which analytic algebra should be included in the exam alongside Euclidean geometry and applied mathematics. Euclidean geometry treats the properties of shapes as they (arguably) exist in the real world. Analytic algebra, invented by Descartes in the 17th century, expresses (arguably) these same truths in mathematical form; that is, the formulas of Cartesian algebra were conceived by most Victorians merely as a translation, or symbolic representation, of the truths already expressed in different form by Euclid. For example, one could express the Pythagorean Theorem as shapes subject to a “proof by rearrangement”; that is, one could measure the physical area of the relevant squares to show that, in fact, the area of square a is equal to that of squares b plus c (Fig. 1).
Euclid proved the Pythagorean Theorem in a somewhat more abstract way, but he did rely on direct manipulation and measurement of theoretically “real” shapes in space.
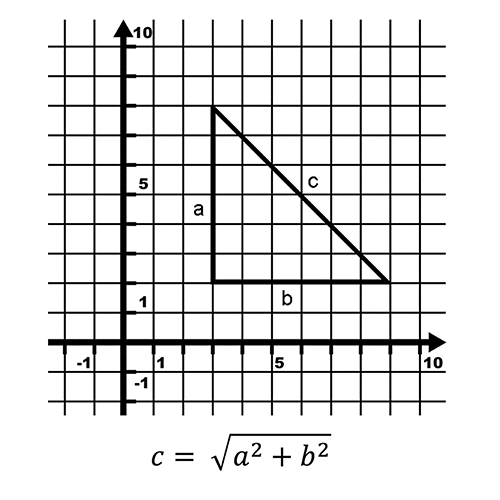
Analytic geometry, on the other hand, expresses values using algebraic equations involving the Cartesian coordinates of the points lying on the shape.
So in this case, in order to find the length c, we would use the formula that expresses the Pythagorean theorem algebraically. This version of the theorem is also subject to proof within the constraints of the Cartesian system—there are many dozens of other algebraic proofs as well, all of which manipulate numbers rather than shapes. (The theorem can also be proved using trigonometry, differential calculus, etc.) But it is Cartesian coordinate (or analytic) geometry, which we hardly consider controversial or cutting-edge now, that caused a great deal of consternation for the Victorians.
The issue for these Victorian thinkers is that, once the seemingly self-evident truths of Euclidean geometry are translated into a purely symbolic and abstract system, a representational crisis occurs: what is the guarantee that the system, even if internally coherent, corresponds to anything in reality? As long as analytic geometry confines itself to expressing truths that can also be accessed using Euclidean geometry, and the two systems correspond, the crisis is dormant. But theoretical problems presented themselves in the nineteenth century that threatened this easy correspondence.
One important challenge came from the introduction of negative numbers, which were not accepted by European mathematicians until the latter decades of the nineteenth century. (In fact, the entire Cartesian grid coordinate system was unknown to Descartes himself, who used only one graphical axis in the appendix to his 1637 Discourse on Method, entitled La Géometrie, and did not fully accept negative numbers.) Of course, algebraic problems would sometimes yield negative results, but these were generally considered to be errors or were ignored altogether. The fact that analytic algebra could yield negative results—which do not “exist” in the “real world”—was cause of the first rumblings of concern about its ontological status.
The British mathematician Augustus De Morgan was one of the first to express this concern explicitly; according to historian Joan Richards, as early as the 1830s he “entertained the possibility that algebra might entail simply an internally consistent symbolic development which was more or less susceptible to any particular interpretation” (45). In his 1835 review of George Peacock’s Treatise on Algebra, he acknowledged that this view “at first sight . . . seemed to us like symbols bewitched, and running about the world in search of meaning” (qtd. Richards 45). His anxiety in this regard led him eventually to develop a tripartite canon of algebraic truth: “a symbol is defined when such rules are laid down for its use as will enable us to accept or reject any proposed transformation of it, . . . explained when such a meaning is given to it as will enable us to accept or reject the application of its definition, . . . and interpreted, when, having occurred as a result of explained elements, used under prescribed definitions, a necessary meaning can be given to it” (DeMorgan 174; qtd. Richards 45-6). According to Richards, this was basically a last-ditch attempt to tether analytic algebra to the perceptual world of Euclidean geometry, and to guarantee that it would remain a descriptive discipline, an attempt that was buttressed by such figures as William Whewell, who wrote in 1854 that “mere analytical reasoning is a bad discipline of the intellect, on account of the way in which it puts out of sight the subject matter of the reasoning” (Whewell 45; qtd. Richards 41-2).
However, this position came under continual strain over the course of the next few decades, as mathematicians continued to manipulate the equations of analytic algebra to obtain results that could not exist in the natural world. These challenges were found, for example, in the work of Duncan Gregory and William Walton, who argued that curves generated by the manipulation of imaginary numbers were important to understanding the relationship between analytic algebra and geometry. These ideas were to come under attack by the Irish mathematician George Salmon, who characterized them as no better than “mathematical puns.” Eventually a détente of sorts was reached by De Morgan himself, who proposed that the discipline be divided into the branches of “algebraic geometry,” where “spatial structures would define the limits of the investigation,” and “geometric algebra,” where equations would be the primary subject matter (Richards 53).
Crisis was averted temporarily, but other challenges to the binding of analytic algebra to Euclidean space were brewing. First of all, algebraic equations were beginning to yield problems that seemed to demand the addition of another spatial dimension for their resolution. Several mathematicians, such as George Salmon and Arthur Cayley, began delicately to suggest that the development of n-dimensional geometries, or “hyperspace philosophy” as it was called, might be necessary. As Richards emphasizes, these early suggestions assiduously avoided even hinting at the actual reality of four- (or greater-) dimensional space. But by the time William Spottiswoode addressed the British Association for the Advancement of Science in 1878, the question of the reality of n-dimensional space was rather more mazy:
[Hyperspace] is not seriously regarded as a reality in the same sense as ordinary space; it is a mode of representation, or a method which, having served its purpose, vanishes from the scene. Like a rainbow, if we try to grasp it, it eludes our very touch; but like a rainbow it arises out of real conditions of known and tangible quantities, and if rightly apprehended it is a true and valuable expression of natural laws. (Spottiswoode 22-3; qtd. Richards 58)
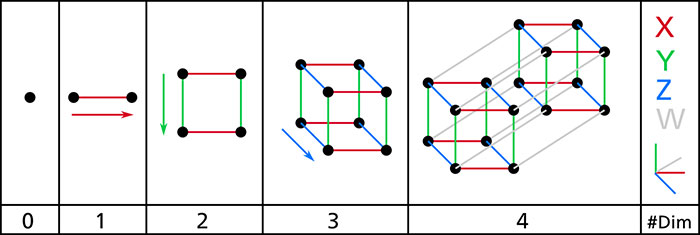
Higher-dimensional geometries, which it is important to remember are Euclidean, can be conceived of quite literally as extensions of “ordinary” three-dimensional geometry. The n-dimensional shape corresponding to the dimension n is generated by a projection of the shape of dimension n minus 1 (Fig. 3).
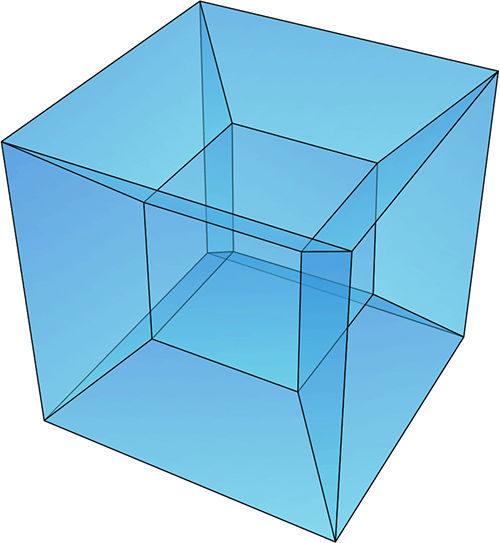
Just as the cube is an extension, in the third dimension, of a square, the hypercube is simply an extension, in the fourth dimension, of a cube.
If each dimension is an extension, or spatial analogy, of the one before, then in theory one could continue to generate (at least mathematically) greater and greater dimensional spaces ad infinitum.
In England the most important popularizer of n-dimensional geometries was Charles Howard Hinton, who expressed this analogical insight in explicitly mathematical terms:
If there is a straight line before us two inches long, its length is expressed by the number 2. Suppose a square to be described on the line . . . this figure is expressed by the number 4, i.e., 2 x 2 . . . generally written 22.. . . If on the same line a cube be constructed, the number of cubic inches in the figure so made is 8, i.e., 2 x 2 x 2 or 23. . . . The question naturally occurs, looking at these numbers 2, 22, 23, by what figure shall we represent 24? (“What Is” 9-10)
“By what figure shall we represent?”: Hinton’s question attempts to argue backwards from the terms of analytic algebra to the natural, “real” world—no longer is the Cartesian system meant merely to represent an a priori synthetic truth (of Euclidean space) translated into other language, but instead is taken as the ground of truth that must reveal something about that space that is not otherwise accessible to us through sensory or other means, that must itself be represented by some figure in the “real” world. As Elizabeth Throesch puts it, the “concept of the fourth dimension of space grew out of a slippage between the languages of these two forms of mathematics, a hypostatization of abstract symbols” (“Nonsense” 41).
Non-Euclidian Geometry: “Non-Euclidean geometry,” as opposed to n-dimensional geometry, refers to those mathematical systems that deny the necessity of Euclid’s fifth axiom, the parallel postulate, which reads: “If a straight line (a) falls on two straight lines (b and c) in such a manner that the interior angles on the same side (alpha and beta) are together less than two right angles, then the straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.” This postulate has been causing headaches for mathematicians for thousands of years. First of all, it is radically more complicated in its form than Euclid’s first four postulates—which read, for example, “Let the following be postulated: To draw a straight line from any point to any point”—and this complexity was felt to undermine the simplicity and self-evident nature of the Euclidean system (see Richards 62-6). For two thousand years, mathematicians attempted to derive the fifth postulate from the first four without success. The reason these attempts were so frustrating is that, while it became clear that the truth of the parallel postulate cannot be proved using only the first four of Euclid’s axioms, neither can his system proceed without a rigorous definition of parallel lines.
As Richards and other historians have demonstrated, many of these failed attempts tried to prove the necessary truth of the parallel postulate by disproving all possible alternatives. Finally, in the early decades of the nineteenth century, several Continental mathematicians decided to take a different tack and explore what ensues when one suspends, as it were, the parallel postulate: two logically consistent geometries result, the hyperbolic and the elliptical.
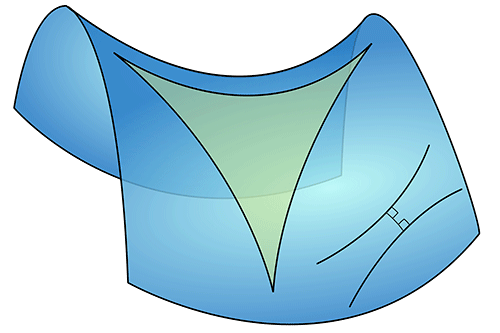
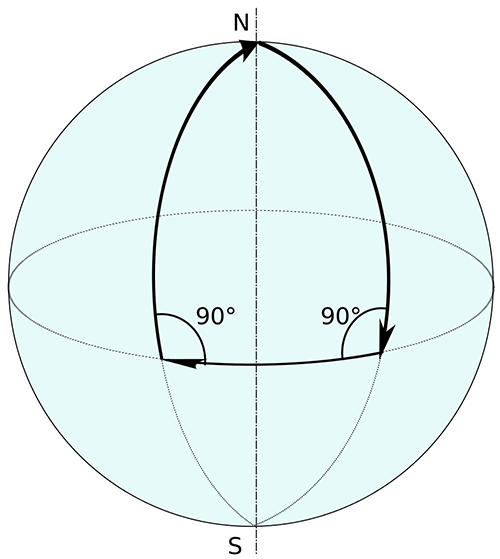
In hyperbolic or acute geometry (Fig. 5), the angles of a triangle add up to less than 180 degrees, and the parallel lines of Euclidean space curve away from each other and are referred to as “ultraparallels.” In elliptical or obtuse geometry (Fig. 6), the simplest version of which is geometry on the surface of a sphere, the angles of a triangle add up to more than 180 degrees, and what would be parallel lines in Euclidean space do intersect.
As Richards argues, the earliest theorists of non-Euclidean space, the Continental mathematicians Janos Bolyai and Nicholai Lubachevsky, were quite explicit that their systems mounted an ontological challenge to the purported reality of Euclidean space—and we can say, by extension, a challenge to the distinction between contingent truth and necessary truth, the hallmark of which had always been the self-evident nature of Euclidean axioms. English mathematicians, who assimilated Bolyai and Lubachevsky’s ideas decades later, in the 1860s, were rather more diffident about the ontological truth-value of these non-Euclidean spaces. To complicate matters further, the German scientist Herman von Helmholz, writing in English to an English audience, used the analogy of two-dimensional space to depict, again by analogy, what the experience of creatures living in a non-Euclidean curved space might be like. He begins by noting that a group of “intelligent beings, living on and moving along the surface of . . . an infinite plane” would “acknowledge the truth of the axioms of Euclid” (128). Creatures who lived on the surface of a sphere would also believe the axioms of Euclid to hold true at “infinitely small dimensions,” but when extended far enough their geometry would differ radically from both our experiential geometry and that of the inhabitants of the plane, as the “shortest lines which the inhabitants of a spherical surface could draw would be arcs of great circles” (128). His discussion then moves on to include the experience of creatures living in other types of space, including space with negative curvature.
Helmholtz begins his discussion with the thought experiment about two-dimensional creatures as a heuristic: “These results regarding surfaces or spaces extended in two dimensions only can be illustrated . . . because we live in a space of three dimensions and can represent in our ideas, or model in reality, other surfaces than the plane (on which alone the geometry of Euclid holds good).” It is easier to imagine geometries of curved space in two dimensions because our brains have difficulty picturing them in three: “When, however, we try to extend these researches to space of three dimensions, the difficulty increases, because we know in reality only space as it exists, and cannot represent even in our ideas any other kind of space” (129). In other words, the flat-plane example was not meant to imply that the geometries of four or more spatial dimensions (which are Euclidean) encompass the same sets of epistemological issues as (non-Euclidean) geometries of curved space, but because his discussion of the latter, in this general-readership journal, relied on illustrative examples from the former, the two “new” geometries became intermingled in popular consciousness.
It was thus this thought experiment that led more or less directly to the consideration of the actual existence of both non-Euclidean and higher-dimensional spaces in the popular imagination. As K. G. Valente notes, Helmholtz’s “illustrative scenario was meant in part to show how one could understandably mistake our space as Euclidean (or ‘flat’) based on small-scale experiences or observations. It gave rise, however, to a commonly held misconception: if the three-dimensional space of our experience might conceivably be curved . . . then analogy suggested it was embedded in four-dimensional space. Consequently, promoting non-Euclidean models of space in the 1870s simultaneously, if unintentionally, served to draw attention to the fourth dimension” (“Who Will Explain” 130).
The main satirical thrust of Flatland, one of the immediate results of this new attention paid to the fourth dimension, is the inability and unwillingness of us Spacelanders to countenance the idea of higher dimensions, because it seems to contradict either the empirical evidence of our senses, or our idealistic epistemologies and metaphysics, or both. On the one hand, non-Euclidean and higher-dimensional geometries challenge the idealism of Kant, who had asserted that our certainty of the truth of Euclidean axioms implies that they constitute a synthetic a priori truth—that is, our knowledge of Euclidean space is not given by experience, and yet it is necessarily true and in fact conditions the very possibility of our experience of the world. The new geometries presented a strong challenge to this notion. Yet the new geometries also threaten faith in empirically derived data as well. This was the crux of the initial waves of debate over the higher-dimensional geometries in the mid-nineteenth century: if the manipulations of algebraic geometry, in which it is possible (and even necessary) to include four or even more dimensions, are not merely theoretical constructs but actually correspond to an unperceivable range of higher dimensions in reality, then the empirical evidence of our senses is also not to be trusted. (As some Victorian mathematicians and philosophers argued, and ultimately Einstein’s theory of general relativity proved to be the case, it might turn out that empirical space is actually non-Euclidean.)
So, on the one hand we have the anxiety attendant upon the notion that analytic algebra might not correspond to the real world (De Morgan’s “symbols bewitched”) and, on the other, the anxiety attendant upon the idea that it does (a position uncomfortable to idealists and empiricists alike). The question basically boiled down to the relationship between algebraic and spatial geometries: was the former an actual representation of the latter, or merely a free-floating internally consistent system of signifiers with no necessary relationship to an external, empirically verifiable world?
Abbott is arguably in the first camp. His character, A Square, is adamant about the actual reality of the third dimension and, in fact, is so bold as to suggest that since a third dimension has been empirically proven to him to exist (in the story, the Sphere actually physically “lifts” A Square into Spaceland in order to show him the true three-dimensionality of space), then why could it not be the case that there are four, five, six, or even more dimensions that actually exist but are unperceivable from our bounded world? The analogy is clear: Abbott is at pains to point out the hidebound limitations of those who will not admit the possibility of the actual existence of higher dimensional space.
While Flatland is certainly the best-known and most influential literary treatment of these abstruse mathematical questions, Abbott was not the only Victorian writer to incorporate encounters with other-dimensional worlds in his fiction. Charles Howard Hinton himself was the author of several “scientific romances” about higher-dimensional worlds, in addition to numerous essays on the topic. He believed in the literal existence of higher dimensions and was a tireless spreader of the gospel. In his 1888 treatise A New Era of Thought, he coined the term tesseract to refer to four-dimensional “hypercubes,” and advocated practicing with a series of actual cubes — which were described in that work and then later published as a fold-out plate in The Fourth Dimension (1904) — until one could visualize higher dimensions.
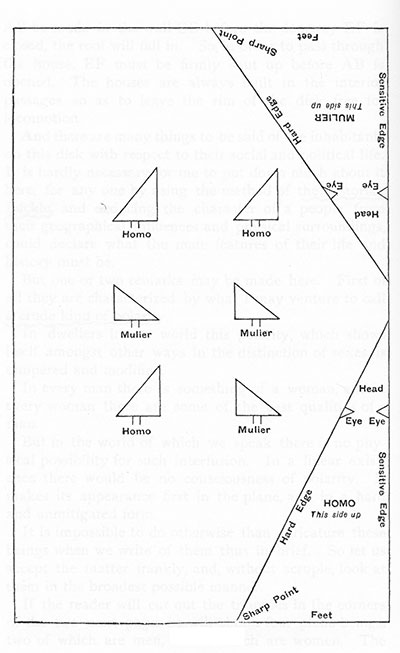
In his fictional tale “A Plane World,” which describes two-dimensional figures living on a flat surface, the heteronormative domesticity of Victorian culture is literalized so that it is the only social configuration that is physically possible. He depicts plane-figure men (“Homo”) and women (“Mulier”) as opposite-facing triangles containing a “hard edge,” a “sensitive edge,” and a “sharp point,” and explains that only triangles of opposite gender can thus comfortably consort with one another: “It is evident that the sharp point of one man is always running into another man’s sensitive or soft edge. Each man is in continual apprehension of every other man. . . . In this land no such thing as friendship or familiar intercourse between man and man is possible” (145). But when “Homo and Mulier be placed together, a very different relationship manifests itself. They cannot injure one another and each is framed for the most delightful converse with the other. Nothing can be more secure from the outside world than a pair of approximately the same height; each protects the sensitive edge of each, and their armoured edges and means of offence are turned against all comers, either in one direction or the other” (146).The central action of the story is a bizarre incident in which Mulier is “suddenly, in all outward respects, turned irremediably into a man” (146). Mulier has learned how to access a higher—in other words, the third—dimension, has lifted up off the plane surface of their world, and accidentally flipped over before re-descending; she has thus undergone a sort of accidental and unwanted gender reassignment. She and her mate are extremely disturbed by this accident, and “one day, with fear, she said that she would either die or be restored to the outward semblance of her sex” (147).
Interestingly, Mulier had gained the ability to access the third dimension in the pursuit of “certain abstruse studies” (146); after her adventure she “manifested a strange knowledge of the anatomy of the race, and most of their medical knowledge dates from her. But no persuasion would induce her to reveal her secret; all the privacy of existence would be gone, she said, if she revealed it” (147). Both Hinton and Abbott are quite concerned, in their higher-dimensional fictions, with the preservation of Victorian notions of domestic privacy and secrecy in other-dimensional worlds. One of the most striking incidents in Flatland occurs when the three-dimensional emissary Sphere elevates Square above the surface of Flatland, and they fly over the landscape and look down into the latter’s own house: “I looked below, and saw with my physical eye all that domestic individuality which I had merely inferred with the understanding. . . . All this I could now see” (96, emphasis in original).
The real anxiety for the Victorian hyperspace fabulists and their readers is that, by extension, privacy in our three-dimensional world is equally vulnerable to invasion. The flying scene in Flatland continues when A Square goes on to reason, by analogy, that there must be even higher dimensions from the perspective of which there is no privacy for Spacelanders. As he asks Sphere after the end of their journey:
[E]ven as we, who are now in Space, look down on Flatland and see the insides of all things, so of a certainty there is yet above us some higher, purer region . . . from the vantage-ground of which we shall look down together upon the revealed insides of Solid things. . . . Doubtless we cannot see that other higher Spaceland now, because we have no eye in our stomachs. But . . . of a surety there is a Fourth Dimension, which [can be] perceive[d] with the inner eye of thought. (102-04, emphasis in original)
Ironically enough, Sphere recoils in horror at the thought, doubling the thrust of Abbott’s satire about the great difficulty of moving beyond hidebound notions and opening up to new scientific and philosophical ideas.
In H. G. Wells’s “The Plattner Story,” this posited omniscient view—and invasion of domestic privacy—does in fact occur when a mild-mannered three-dimensional man is vaulted into the world of four dimensions. The main action of the story takes place when Plattner is transported at random to a domestic scene peopled by strangers. One night he is wandering about in this new world when he is “arrested by the sight of the thing that was happening in a room in a back street. . . . The windows were open, the blinds up, and the setting sun shone clearly into it, so that it came out quite brightly at first, a vivid oblong of room, lying like a magic-lantern picture” (24). What he sees is a man in bed, clearly dying, while a woman frantically rustles through some papers in a cabinet in the corner of the room. The scene is both domestic and dramatic, in a Middlemarchian sort of way. Plattner has visual access to this (and other) scenes, but no other kind of contact is possible—no one can hear or see him, and figures pass right through him unheeding as if he, or they, were ghosts. His role is strictly observational; one might say omniscient-narratorial. Later the narrator informs us that he (the “author”) has exercised remarkable restraint in not embroidering this incident for greater dramatic purpose: “I have resisted, I believe successfully, the natural disposition of a writer of fiction to dress up incidents of this sort. . . . I have carefully avoided any attempt at style, effect, or construction. It would have been easy, for instance, to have worked the scene of the death-bed into a kind of plot in which Plattner might have been involved” (27-28).
Perhaps the particular historical moment in which these tales were written, the last decades of Victoria’s reign, is particularly suited to nostalgia for a world of perfectly fitted geometric creatures forming a literal interiority. For all of these hyperspace writers, the gutting of privacy and bodily integrity—in other words, of domesticity—has recompense in a greater understanding of the nature of the universe as fundamentally complete; the nostalgia goes hand in hand with a compensatory fantasy of the power of the same knowledge which has effected the demise of secrecy; as Hinton ruminates, “Any one, who will try, can find that, by passing deeper and deeper into absolute observation of matter, and familiarity with it, that which he first felt as real passes away. . . . Thus there springs before the mind an idealism which is more real than matter; a glimpse of a higher world, which is no abstraction” (“Many” 42).
published May 2016
HOW TO CITE THIS BRANCH ENTRY (MLA format)
Kreisel, Deanna. “The Discovery of Hyperspace in Victorian Literature.” BRANCH: Britain, Representation and Nineteenth-Century History. Ed. Dino Franco Felluga. Extension of Romanticism and Victorianism on the Net. Web. [Here, add your last date of access to BRANCH].
WORKS CITED
Abbott, Edwin A. Flatland: A Romance of Many Dimensions. 1884. Ed. Rosemary Jann. Oxford: Oxford UP, 2006. Print.
DeMorgan, Augustus. “On the Foundation of Algebra.” Transactions of the Cambridge Philosophical Society 7 (1842): 173-87. Print.
Helmholtz, H. “The Axioms of Geometry.” The Academy (12 Feb. 1870): 128-31. Print.
Hinton, C. H. “Many Dimensions.” Scientific Romances 2nd. Ser. 1896. London: Swan Sonnenschein & Co., 1909. 27-44. Hathi Trust. Web. 30 November 2013.
—. A New Era of Thought. London: Swan Sonnenschein & Co., 1988 Print.
—. “A Plane World.” Scientific Romances 1st. Ser. 135-56. Print.
—. “What Is the Fourth Dimension?” Scientific Romances 1st. Ser. 3-32. Print.
Richards, Joan. Mathematical Visions: The Pursuit of Geometry in Victorian England. Boston: Academic Press, 1988. Print.
Spottiswoode, William. “Presidential Address.” Report of the Forty-Eighth Meeting of the BAAS Held at Dublin in August 1878. London: John Murray, 1879. 1-32. Print.
Throesch, Elizabeth. “Nonsense in the Fourth Dimension of Literature: Hyperspace Philosophy, the ‘New’ Mathematics, and the Alice Books.” Alice Beyond Wonderland: Essays for the Twenty-First Century. Ed. Christopher Hollingsworth. Iowa City: U of Iowa P, 2009. 37-52. Print.
Valente, K. G.. “‘Who Will Explain the Explanation?’: The Ambivalent Reception of Higher Dimensional Space in the British Spiritualist Press, 1875-1900.” Victorian Periodicals Review 41.2 (2008): 124-49. Print.
Wells, H. G. “The Plattner Story.” The Plattner Story and Others. London: Methuen & Co., 1897. 1-28. Archive.org. Web. 10 September 2013.
Whewell, William. Of a Liberal Education in General. London: John W. Parker, 1845. Print.